Geometric distribution
date posted: 2020-06-13
Contents
What is discrete probability distribution?
For me I tend to break down thing to understand the concept. What is a probability distribution?
It is a way of representing "probability" for each possible outcomes in given experiment.
In a given experiment if number of possible outcomes are infinitely many it is called a continuous proability
distribution.
When there are finite number of possible outcomes discrete probability distribution.
Putting them together it is way of representing probability of all possible outcomes in an experiment with
finite number of outcomes such as rolling a die, picking a card from a deck, etc...
rolling one die
For example when rolling a die there are number of outcomes(discrete), and if you calculate probability of rolling 1, 2, 3, ..., 6(all possible outcomes), you have a discrete probability distribution. It is mathematical function that outputs proability of it input occuring. So if you input 1 discrete probability distribution will output 1/6 which is probability of rolling a 1.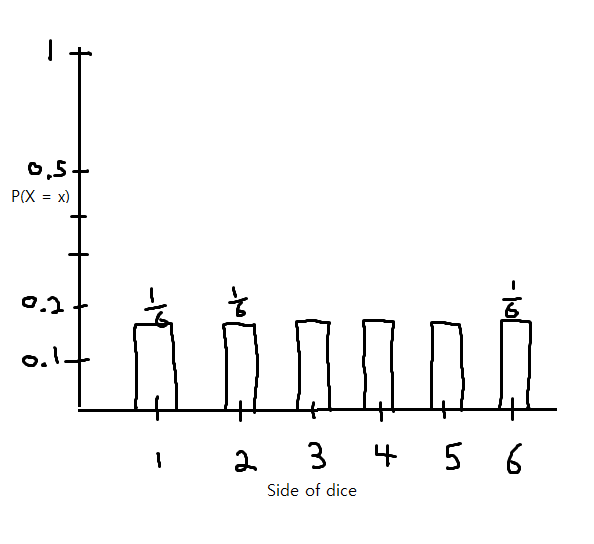
P(X=x) is a notation for proability of random variable x happening. P(X=1) = proability of rolling a 1.
For all random variable (possible outcome) they have same proability of 1/6 therefore it is called a uniform distribution.
Next we will look at discrete probability distribution of rolling two dice.
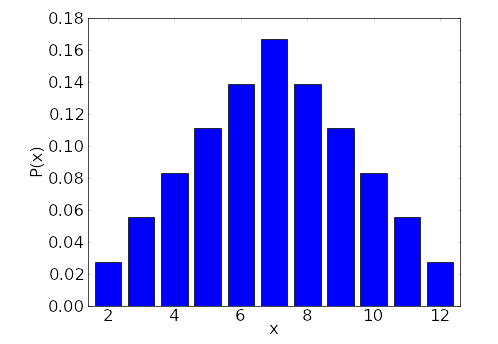
rolling two dice.
Below is probability distribution of rolling two dice. x-axis represents possible outcome from two rolls. Given x we can find its probability just by looking at the distribution.
Two examples above seem very intuitive that creating a formula may seem cumbersome.
What if someone asks you for the probaiblity of rolling
a die 100 times and getting 1 for the first time? It is not very intuitive, but with help of discrete probability distribution we can make in more intuitive
and by help of special types of discrete probability distribution it will make calculations easier.
Main objective of creating a formula is to not re-invent the wheel, we can use generalized formula over and over again on similar questions.
Geometric distribution
Geometric distribution is a special type of discrete distribution used for solving specific problem such as
finding proability of first success.
To use geometric distibution it must satisfy two conditions:
- independent trials --> previous trial does not affect next trial's outcome.
- Binomial outcome --> like "yes" or "no, only two possible outcome.
Example question:
Q: Your goal is to roll 10-sided die and find proability of rolling a 1 after 7 tries.
1. Rolling a die are independent trials since rolling one die would not affect outcome of next roll.
2. People might be saying that there are 10 possible outcomes therefore it does not satisfied 2nd condition. However
we could make this into a binomial outcome. Since we are interested in rolling a 1, other than 1 we treat it as "fail" therefore
rolling 1 = "success" and others = "fail".
First thing you need to do is calculate probability of success and failure.
- In our case success = rolling a 1. Since it is 10-sided die probability of rolling a 1 would be 1/10 = 10% denoted as p = 0.10.
- Any other outcome would be a failure therefore 1 - 0.1 = 0.9 = 90% denoted at q = 0.9.
Then we generate general formula for finding probability of success at r trial. (r is just an integer)
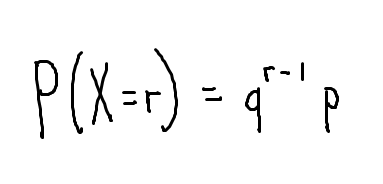
X stands for random variable in our case number of trials denoted by r. p = success probability and q = failure probability.
P(X=1) = proability of succeeding in 1st trial = (q^r-1)p = (0.9^0)(0.1) = 0.1 which makes sense since rolling a 1 is 1/10.
P(X=2) = proability of succeeding in 2nd trial, and by using this formula we could find probaility of any P(X=r).
Simply you could think of P(X=r) as "how many times do I need to fail in order to succeed on rth trial?" so P(X=9) would mean I need to fail 9-1=8 times thus q(probaility of fail)^8 then after 8 failure you will succeed therefore multiply probaility of success hence we get the formula P(X=r) = q^(r-1)p
Geometric distribution often depicted using a tree
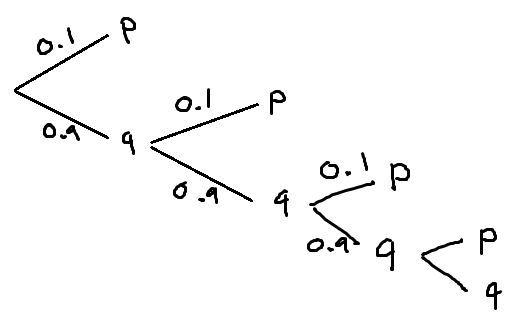
Using above tree, if you fail once then succeed you move down to q then to p thus (0.9)(0.1) if you fail two times then succeed it would be (0.9)(0.9)(0.1).
Now we can answer our question. P(X=8) = (q^8-1)(p) = ((0.9)^7)(0.1) = 0.0478. Probability of rolling a 1 after 7 tries is 4.7%.
Next we will look at another special discrete probability distribution called Binomial distribution.