Binomial distribution
date posted: 2020-06-21
Contents
Binomial distribution
Even though I am a math major I find statistics more fun to study since many theorems appear in real life unlike mathematics where most problems are abstract. Today we will talk about Binomial distribution which is used to solve many practical problems in real life. When young, most people probably have been questioned "What is the proability of flipping 3 heads in 5 flips?" or something similar. Not many knew the answer or even if they did they could not solve similar questions that involved higher number of trials and successes.
This is exactly where Binomial distribution can help. It is a special type of discrete probability distribution, for those of you who do not know what discrete proability distribution is, refer to previous blog on Geometric distribution.
Binomial distribution is probability distribution of binomial random variable. Say you are flipping 10 coins(binomial experiment) and want to find out probabilty of getting "r" number of heads where "r" is any positive integer between 0~10. You would calculate probability of getting 1 heads in 10 toss, 2 heads in 10 toss, 3 heads in 10 toss and so on... number of heads are denoted as X, which are referred to as random variable. Distribution of these random variables are called probability distribution of such experiment.
Three conditions must be satisfied for probabilities of random variables to exhibit behavior of binomial distribution.
- All trials must be independent and have equal success rate
- Each trial is binomial experiment (having only two outcomes)
- Fixed number of trials.
Deriving formula for binomial distribution
Let's say a I have 30% chance of making a 3-pointer, which automatically assign failure percentage of 70%. I want to know the probability of making 2/5 3-pointers.
Probability of scoring 2 shots and missing 3 shots can be interpreted as (0.3)(0.3)(0.7)(0.7)(0.7) since probability of scoring is 0.3 and missing is 0.7. Denoting scoring as S, misses as M give us SSMMM but there are multiple ways of scoring two 3-pointers. It can be SMMMS, SMMSM, SMSMM, and so on...
So probability of scoring 2/5 must be multiplied by number of ways it could be scored.
Number of ways two 3-pointer could be scored can be calculated using combinatorics.
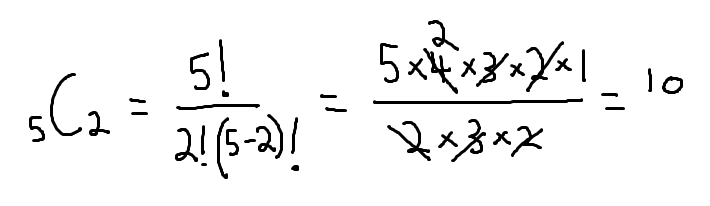
There are 10 different ways two 3-pointers can be made in 5 tries. Now multiplying it with probability of making 2 shots and missing 3 shots
would be
 which equals to 0.3087 = 31%. I would make 2/5 3-pointers with 31% chance.
which equals to 0.3087 = 31%. I would make 2/5 3-pointers with 31% chance.
We always want to generalize our formula so we don't reinvent the wheel.
Notice that # of ways 2 shots can be made in 5 tries was represented as 5C2 so if we want to
find # of ways "r" shots can be made in "n" trials our formula can be generalized to nCr.
We know that probability of success is often denoted as p and failure as q = 1-p.
Combining them we get generalized formula for binomial distribution.

Example question
Q: Find the proability of getting 2 heads in 6 coin flips?
n = 6, total number of trials. Flipping heads is considered a success meaning flipping tail is considered failure. Each trial is independent and has equal probability of success therefore it satisfies first two conditions of binomial distribution. Lastly since we are working with fixed number of trials we satisfy all three conditions allowing us to use binomial distribution formula.
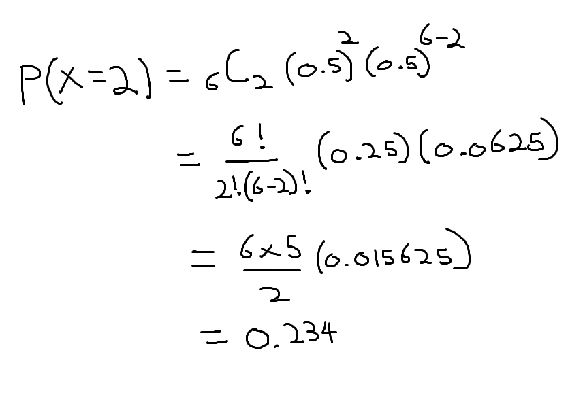
A:Probability of getting 2 heads in 6 coin flips is 23.4%
Cumulative Binomial distribution
Previous example only considers finding probabiliy of exact random variable. If we want to find probability of getting 2 or 3 heads in 6 coins flips we simply add P(X=2) + P(X=3).
To find probability of getting 3 heads or less we simply add all probabilities of random variable 0,1,2,and 3.
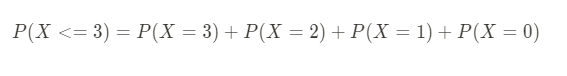
Limitation
Very simple right? Now we know how powerful binomial distribution is. Time to look at some of its limitations.
Let's say you want to find probability of getting less than or equal to 50 heads in 100 coin flips. We could do it by applying stuff we just learned however there are 51 different probabilities you need to calculate and sum together which can be very cumbersome and prone to error. As number of trials and successes gets larger it would be hard if not impossible to calculate without a program. In 2020, we have computers however they did not during development of statistics therefore they needed a way to mitigate this limitation.
Next, I will explain how limitations of binomial distribution can be alleviated by help of normal distribution.