Insertion Sort:
date posted: 2019-12-25
Very similar to bubble sort in terms of complexity of implementing it and how to derive time complexity. One main difference is that in insertion sort at each iteration, one more element will be added to compare.
Say we want a list [25, 17, 31, 13, 2]
- Starting from first element, treat it as new list with one element. As you can see in the drawing below, now you have one list [25], we will call it sorted list and other one unsorted list.
- Our goal is "insert" each element from unsorted list into sorted list. Starting from first element in unsorted list 17 compare it with last element in sorted list 25. Since 17 < 25 move 25 to its right and insert 17 into newly opened position.
- Now compare first element from unsorted list with last element in sorted list. Since 25 < 35 and we know that sorted list's last element is highest, insert 31 in last position.
- Now we have sorted list with 3 elements, repeat this process until all elements in unsorted lists are inserted into sorted list.
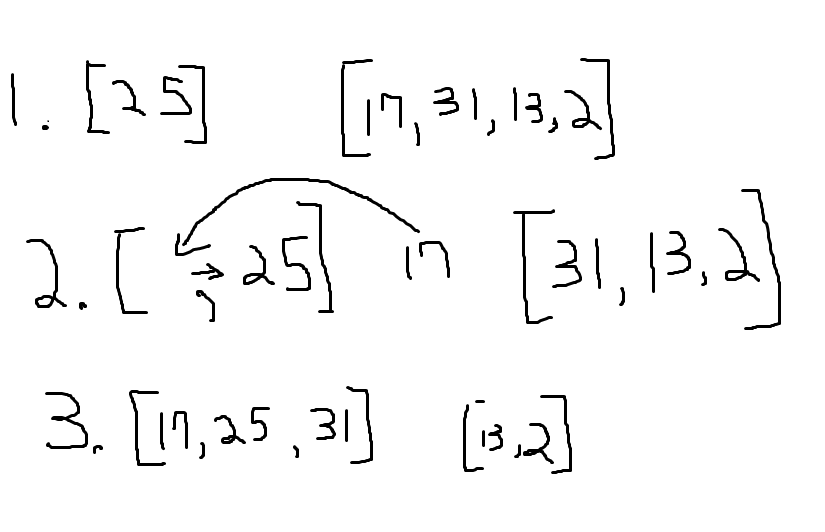
Time Complexity:
If you want how to prove time complexity, check out bubble sort, here I will just explain time complexity.
Using our example up top, when we get list with five elements we start by inserting an element in sorted list. Now we compare elements from unsorted list with element in sorted list.
First, there is one element in sorted list thus only one comparison can be done.
Next, there are two elements and in worst case where element from unsorted list is smaller than both elements in sorted list there has to be 2 comparision.
Each time if you think about worst case (element from unsorted list having lowest number) number of comparison increase by 1. At the end you will compare 4 elements (n-1). So in our example, each time you compare 1, 2, 3, and 4 times. Say you get n length list then number of comparisons will be 1, 2, 3, ... , n-1
This is exact opposite of bubble sort which is n-1, n-2, ..., 3, 2, 1. Thus there time complexity are exactly the same in worst case scenario. O(n) = n^2