Bubble Sort:
date posted: 2019-12-22
One of simplest algorithms thus quick to implement. Starting from first element in a list, you simply compare with adjacent element and swap positions accordingly. Move on until you get the largest element at the end of the list and repeat this process until all elements are sorted. Similarily if you want to sort in reverse order start from last element.
There isn't much with Bubble sort therefore let's get straight into example:
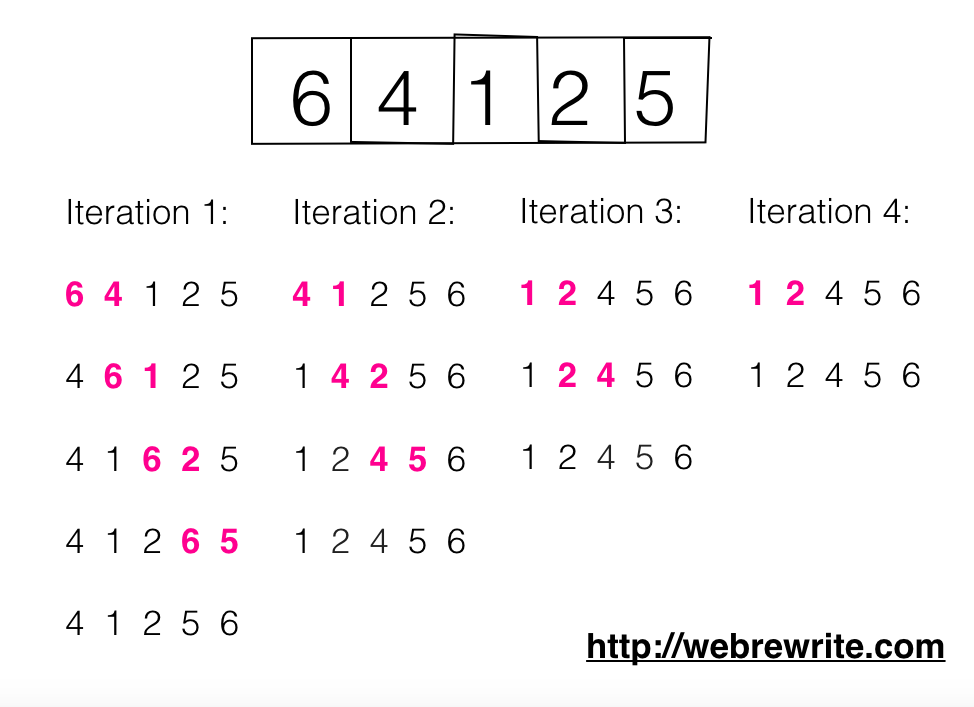
We are going to sort a list = [6, 4, 1, 2, 5]
- We pick our first element, 6. Compare it with its adjacent element 4. Since 6 is greater than 4 we switch positions. Now we have 6 in second position thus compare it with its adjacent element which is now 1. Again since 6 > 1 we switch positions. Repeat this process and we 6 will be positioned at the end of list, our first iterations is done.
- In second iteration we repeat same process as before but now since 6 has been sorted from above iteration our list to sort is [4, 1, 2, 5]. Now with smaller list repeat the process. One thing to note, in 3rd comparision, comparing 4 with its adjacent element 5. They are already in proper position, in such case keep the position and now your comparing element becomes 5 thus next step is to compare 5 with its adjacent element which is 6. Again it is in proper position thus our second iteration has finished as well.
- Repeat above process until list to sort becomes length of one.
Time Complexity:
It is important to know how fast your algorithm is and even better if you know how to prove it.
From above example we start from list of 5 elements. In bubble sort we choose first element and compare it with all the elements, if that element is sorted repeat process but now ignore sorted elements thus there are one less elements to compare.
Starting from 5 element list, first there are 5-1 elements we need to compare. Then 4-1, 3-1 and so on...
let n = length of list. Now for each iteration we compare n-1, n-2, n-3, ...., 2, 1 elements. thus number of comparison in total will be (n-1) + (n-2) + .... + 3 + 2 + 1.
Thanks to gauss we know that 1 + 2 + ... + (n-2) + (n-1) + n = n(n+1)/2
In our case we have up to (n-1) thus our formula becomes
(n-1)(n-1+1)/2 = n(n-1)/2
Therefore our Time complexity is n^2/2 - n/2. But as data gets infinitely large n^2 will increase in
such faster pace that n/2 will have no effect in our formula so finally our
Proof:
Understanding how a formula is derived is key when learning something. It will not only stay intact for a longer time however you will start to appreciate mathematics behind it and hopefully enjoy it.
We want to prove how (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2.
First let f(n) = (n-1) + (n-2) + ... + 2 + 1, which is simply formula for adding 1 through n-1
Add exactly same formula so it become 2f(n) but place them in opposite order.
So one 1. f(n) = 1+ 2+..+(n-1) and
another 2. f(n) = (n-1) + (n-2) ... +2 + 1
They are exactly same formula but ordered differently right?
Here is the fun part:
- Add those formulas together.
- adding first elements together, 1 + (n-1) = n.
- add next elements and again you get, 2 + (n-2) = n.
- if you repeat the process it becomes n+ n + n ... + n
- In each formula there are n-1 elements so n+n+n+...+n = n(n-1). There are n-1 number of n
- since we got that by adding two f(n), 2f(n) = n(n-1).