Heap:

date posted: 2020-01-12

What is Heap?

Heap is a data structure that is complete binary tree with one more additional property. Where parent node has to be either greater or less than their child.

• Max-heap: Complete binary tree where parent node has to be greater then child nodes
• Min-heap: Complete binary tree where parent node has to be smaller then child nodes

A binary tree is a tree where each node consists maximum of 2 nodes. Complete binary tree is a binary tree with one additional condition being that all child tree must be filled up from left to right.

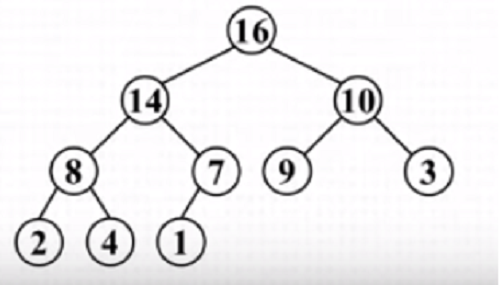
looking at image below we can see:

1. All node has maximum of 2 child thus it satisfies condition of being binary tree.
2. Looking at lowest part of the tree we can see leaf nodes are filled up from left to right thus it satisfies condition of being complete binary tree

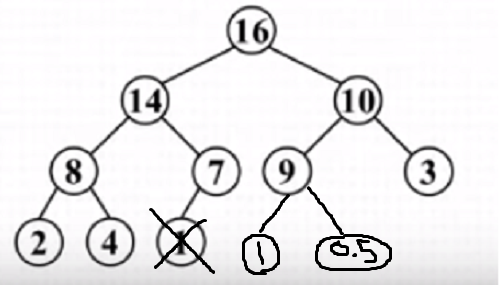
What about this tree below?

1. Just like above tree, all nodes have maximum of 2 child thus it is a binary tree
2. Looking at the lowest part, going left to right we see empty spaces(childs for node 7 is missing) and then more child nodes therefore it is not complete binary tree.

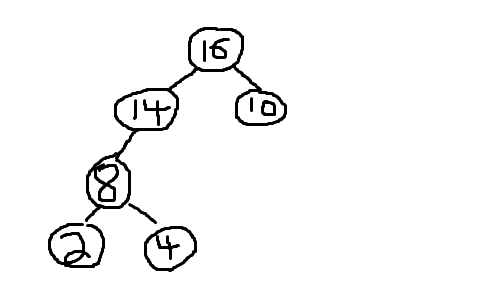
Lastly, looking at the tree below

1. It's a binary tree
2. lowest part are filled from left to right. But before adding 2, 4 as a child node of 8. To be complete binary tree within lowest level it has to go from left to right. So if 2,4 were consequtively inserted into our tree, it would have to be like tree on the right to be complete binary tree.

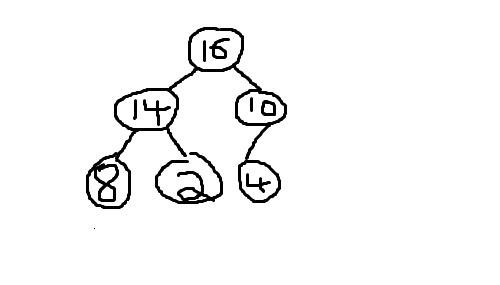
For me, I like to understand the reason for additional conditions. For example from binary tree why did concept of complete binary tree arise and then max/min heaps?

From binary tree, adding addtional condition to create complete binary tree has many implementations and makes our lives easier.

Say you want to implement binary tree in your code using a list. You will need to have rules that assign each node to certain position in a list.

Instead, why not just create a complete binary tree and simply store starting from root node and moving left to right? Using our initial graph of complete binary tree, root node will go in as first element then 14 as second element, 10 as third, 8 as fourth and so on... Finaly looking like [16, 14, 10, 8, 7, 9 3, 2, 4, 1]

Now by adding additional condition we can implement in our code much easier. Furthermore adding additional condition either Max/Min heap orders the list either in ascending or descending order therefore if you always know that first element of max-heap would be highest element in the list. Therefore heap data structures is used in sorting algorithms(heap sort), priority queue, graph algorithms, etc...

Heapify

When you have heap data structure it makes your life easier. However you need to give effort in maintaining its strucutre, we call it heapify. Max-heapify for maintaining max-heap data structure and Min-heapify for min-heap.

For Max-Heapify if you have a parent that has smaller value then their child, simply switch places with bigger child. Repeat this step until no more comparison can be made or max-heap structure is met.

For Min-Heapify if parent has greater value than child switch places with smaller child, and so on...

For clarity let's look at below example and perform max-heapify. We can see it is a complete binary tree but not a Max-heap since bottom node 4 is smaller than both of their child. Following steps explained above.

1. switch place with bigger child, 14.
2. Again, on second picture 8 > 4. So again switch place with bigger child.

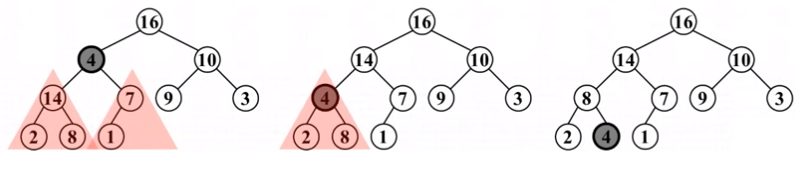
Now You've just maintained Max-heap structure.

Let's write it in Python.

        def max_heapify(lst, length_of_list, i):
            largest = i
            
            l_child = (2*i)+1 
            r_child = (2*i)+2
            
            if l_child < length_of_list and lst[i] < lst[l_child]:
                largest = l_child
            
            if r_child < length_of_list and lst[largest] < lst[r_child]:
                largest = r_child
            
            if largest != i:
                lst[i], lst[largest] = lst[largest], lst[i]
                
                max_heapify(lst,length_of_list, largest)
                
            return lst

        lst = [16, 4, 10, 14, 7, 9, 3, 2, 8, 1]
        length_of_list = len(lst)
        for i in range(length_of_list, -1, -1):
            max_heap = max_heapify(lst, length_of_list, i)
        print(max_heap)

        >>> [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    

Time Complexity

Each time heap structure is not satisfies, just need to move down the binary tree. When heap has n nodes it will have depth of log(n) therefore for n node heap there will be maximum of log(n) heapify. Therefore Time complexity = O(log(n)).