Hash Table:

date posted: 2020-01-19

What is Hash Table?

For me, I find it easy to learn a concept and keep it intact in my memory if I know its full story and their applications. So let's begin with why Hash table were invented.

They were invented to overcome deficiency that Direct Access Tables were facing.
Direct access table is a table where each data has associated index therefore desired data could be directly reached with O(1) time complexity. For example, for each of your friend if you enter their name on your directory all their informations show up, this is direct access table where name is an index.
In mathematical terms its an injective function or one-on-one mapping.

You can easily see that since each index is used to get their data, operations like inserting, deleting, searching all have time complexity of O(1).
Then seems to be the problem?

Even though all operations have exceptional small time complexity, it suffers largely from space complexity. Since for each friend there must be an extra memory space for every index that points to an information of a friend. As list of friends become larger there will be more memory space that aren't often used.

Say there are 100 students in a school where on average 50% of students study in the library, if you want to create a library of 100 seats for each students, half of the seats will not be occupied. On average less than half will not be used and in break times none of them will be used. We could avoid this problem by using concept of Hash Table.

Assign 2 student per desk therefore you only need 50 desks instead of 100. From student_1 to student_100, we use a function called hash function to efficiently assign two students to one desk. In this case we will use modular arithmetics (hash function may not be modular arithmetics) and create hash function denoted h(x) where x represents student number.

h(x) = x mod 50, which returns what is left after dividing x by 50.

• when x = 1, h(1) = 1 mod 50 = 1 => student_1 gets assigned to desk_1
• when x = 2, h(2) = 2 mod 50 = 2 => student_2 gets assigned to desk_2
.
.
.
• when x = 51, h(51) = 51 mod 50 = 1 => student_51 gets assigned to desk_1

So by using this hash function we are able reduce cost of 50 desks

The reason it is called a hash table is because original key is transformed via hash function which is now a key(index) of new table, hash table.

Hash table's time complexity depends on its hash function therefore main goal of using hash table is to use hash function that distribute original keys equally into hash table. If hash function map multiple key into same position then when calling that index multiple values will be returned and from there you must search in linear fashion to find your index. This phenomenon is referred to as collision. When this happens there is two ways of handling them:

1. Chaining: Creating a linked list whenever collision happens. Therefore when trying to search it will have time complexity of O(len(linked_list)).
   benefits:
   • Easy implementation
   • You don't have to know how many keys will be inserted or deleted.
   disadvantages:
   • Since it uses linked list data structure, lacks cache performance
   • Maybe some parts of hash table are not used => space complexity increase w/o being used.
   • In worst case, all keys collide leading to O(n) search time.
2. Open addressing: When collision happens, look for next empty space to store index.
   When searching, first goto assigned index then keep moving onto next hash table's index until wanted index is reached or until there is empty index => information of that index doesn't exist.
   
   One thing to note is its deletion operation. When a key is deleted, its index in hash table is marked as "deleted". Insertion can happen in "deleted" index however while searching, it skips "deleted" index.
   
   

   There are two types of Open addressing: Linear probing and Quadratic probing.

   Linear Probing: basically what I've described above. I will give an example for clarity.

   Until I buy digital drawing pad, lets suffer together...
   Looking at image below: We are passing keys: 3, 4, 7, 10 through hash function h(x) to hash table.

   1. key = 3, h(3) = 3 mod 3 = 0 so it gets assigned to 0th index. All is good.
   2. key = 4, h(4) = 4 mod 3 = 1, gets assigned to 1st index. All is good.
   3. key = 7, h(7) = 7 mod 3 = 1, gets assigned to 1st index. Uh oh, collision! Move to next empty index. All is good.
   4. key = 10, h(10), 10 mod 3 = 1, gets assigned to 1st index. Uh oh, collision! Move to next index. Uh oh another collsion! Now it gets assgined to empty index 3.

   As you can see if all keys maps to index 1. Time complexity of inserting becomes linear which is never good. This is main problem with linear probing and this phenomenon is known as Clustering.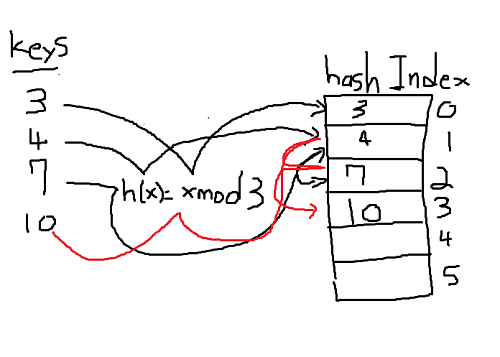

   

   Quadratic Probing: h(x) = (x + i^2) mod k , where i = number of collison.

   For simplicity, lets use quadratic probing on example from linear probing.

   1. h(3) = (3 + (0)^2) mod 3 = 3 mod 3 = 0. Notice since no collision i = 0. Assigned to 0th index.
   2. skip key=4, we are at key=7, h(7) = (7 + (0)^2) mod 3 = 1. Collsion happens so our formula becomes h(7) = (7 + 1^2) mod 3 = 8 mod 3 = 2. Gets assinged to index 2.
   3. key =10, collision at index 1. So h(10) = (10 + 1^2) mod 3 = 11 mod 3 = 2. Uh oh! Second collision. Now our formula become h(10) = (10 + 2^2) mod 3 = 14 mod 3 = 2. Again we have 3rd collision (I didn't expect this...)
      Now, h(10) = (10 + 3^2) mod 3 = 19 mod 3 = 1. Another collsion... But you get the point. You keep adding (number_of_collision)^2 to key value.
   We've just suffered from quadratic probing. It is because quadratic probing must satisfy some requirements to assign every key to every spot. The requirement is that the table size must be:
   • Prime number
   • never be more than half full

   Double Hashing:

   Similar to quadratic probing however here, replace quadratic with another hash function. h(x) = (x + (i x h2(x)) mod k), i = number of collision and h2(x) is another hash function.

In summary, to avoid increase of space complexity we use hash functions but time complexity increases if collision happens so we must create hash table with hash function that minimizes collision.