Shortest path algorithm:
date posted: 2020-02-16
What is shortest path algorithm?
You would probably guess what this algorithm is all about... Yes it is finding shortest path that
takes you from one place to another but it can be done if the graph is
directional acyclic graph. If it is undirected graph you could make it directional
by replacing undirected edge with two directed edge going in opposite direction.
All of the readers probably benefit from this algorithm in
everyday lives when using google map, kakao map to get from current place to another those maps perform
shortest path algorithm.
There are two different types of shortest path algorithm
- Single source: Finding shortest path between your starting point and all other vertices
- All-pairs: Finding shortest path between any pair of vertices in a graph
When you are using single source shortest path algorithm you will know all distance from your starting position to all vertices however you won't know distance between any other pairs of vertices if one of them is not a starting vertex.
In all-pairs shortest path you will know all distance between any pairs of vertices in a graph. So you would know distance going from A-B, B-C, A-C and so on.
Single source
There are two main algorithms that belong to single source shortest path algorithm. Dijkstra algorithm named after Edsger Dijkstra, Bellman-Ford was names after Richard Bellman it is said that this algorithm was first proposed by Alfonso Shimbel in 1955 however Richard Bellman published it in 1956 and Edward F. Moore published the same algorithm in 1957 thus sometimes called Bellman-Ford-Moore algorithm.
Dijkstra
Dijkstra is used when graph is acyclic directed graph with all positive edge weights if graph is undirected you must change it to directed graph by replacing undirected edge with two directed edges going in opposite direction. It does work on edges with negative weights however most of the times it will fail. We will perform Dijkstra algorithm on example with all positive edge weights then on example with negative weight edge to show why it is not suitable.
Dijkstra algorithm follows these steps below:
- Pick a starting vertex, find shortest path to all other vertices from starting vertex. If they are directly connected assign edge weight on top of the vertex else assign infinity as there are no direct path to it => we do not know how to get there.
- Pick vertex that has smallest distance from starting vertex and perfrom relaxation.
- Again select smallest one and repeat step 2.
- Repeat above steps until all vertices are reached.
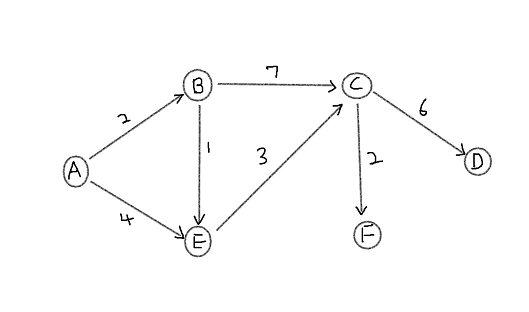
1. Set vertex A as starting vertex, find shortest paths. It has two directly connected vertices B and E therefore distance from A-B is 2 and A-E is 4. All other vertices are not directly connected therefore distance from A are infinite.
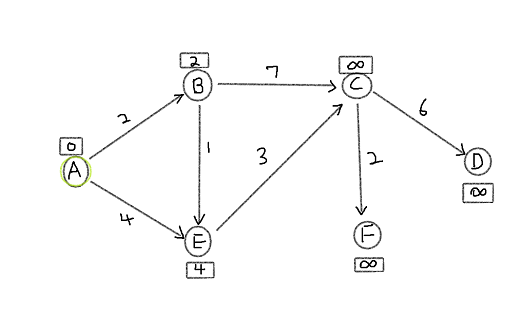
2. Vertex with smallest distance from starting vertex is B. Now look at B's directed connected vertices and perfrom relaxation that is
if (d[u] + w(u,v) < d[v]):
d[v] = d[u] + w(u,v)
# where u = current vertex cost and w(u,v) = cost of u-v edge.
Vertex B has outgoing edge B-E. E already has a distance from starting point that is d[E] = 4. Since d[B] = 2 and
w(B, E) = 1, d[E] > d[B] + w(B,E) is satisfied and vertex E is relaxed to cost 3.
Similarily d[C] = infinity and d[B] + w(B,C) = 9 so d[C] is relaxed to 9.
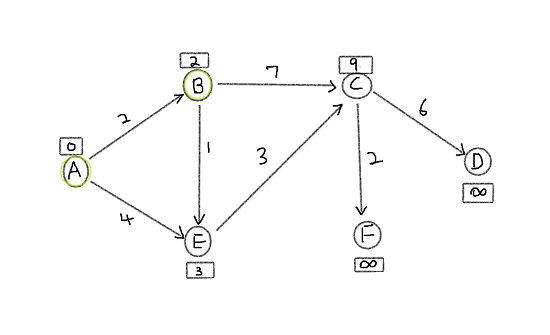
Now we look at E and C. Out of the two E has smaller cost therefore choose E. It has only one outgoing edge to C thus perform relaxation and C is relaxed from 9 to 6. Finally lowest cost vertex is C since F and D have infinite cost. Since both F and D are infinite they are both relaxed to 8 and 12 respectively.
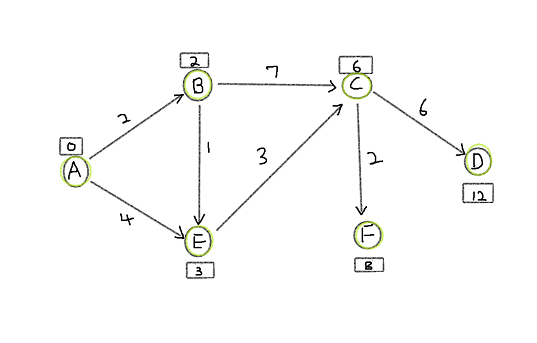
Now we have all shortest paths from vertex A to all other vertices. We have just used dijkstra algorithm to find single source shortest path.
Now by performing dijkstra algorithm on simple example with negative weights see why it does not work.
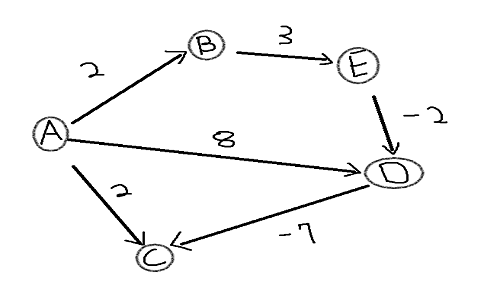
Setting vertex A as our starting vertex and assign distance to all edges.
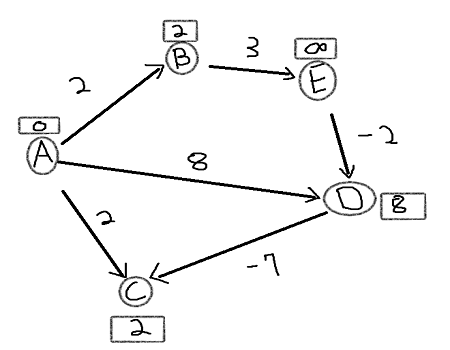
There are shortest path from A-B and A-C with same distance so doesn't matter which vertex we goto first. We will goto B. Shortest path from A-B is set. Next A-C is shortest so shortest path from A-C is set. Next shortest path is B-E = 3 and A-D = 8, since B-E is shorter we move along in that direction and perfrom relaxtion giving shortest path from A-B-E = 5.
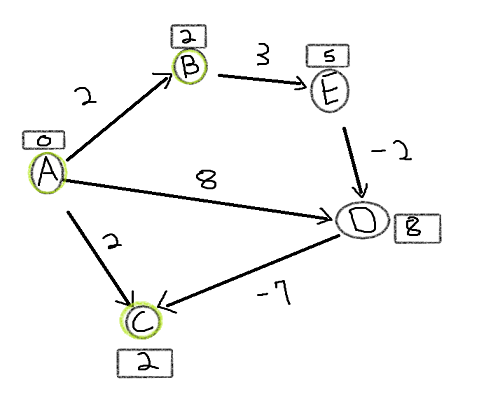
Next shortest path would be E-D which is a negative value. thus giving us shortest path from A-B-E-D = 3. Now we are only left with A-D which has weight of 8 and since we already found shortest path from A-B-E-D, A-D should be greather than A-B-E-D which in fact is so we dijkstra still works with negative weight.

Finally we look at D-C = -7. We've already found shortest path from A-C which was 2 thus by definition of dijkstra if we have found shortest path it cannot be updated thus A-D-C should be greater than A-C. However due to negative weight A-D-C = 1 < A-C = 2 hence shortest path must be updated which is contradictory to dijkstra algorithm since at first dijkstra tells us that A-C is the shortest path going from A to C however later on A-D-C proves that dijkstra algorithm gave wrong answer in the beginning.
Above example shows that sometimes dijkstra works with negative value but sometimes it doesn't.
Now we will look at how to find shortest path with negative weights without ever failing.
Bellman-Ford
Bellman-Ford algorithm can be done in 3 simple steps:
- Create a list containing all edges.
- Initialize distance from start to all other vertices to infinite. Distance from itself is 0.
- Perform relaxation on all edges in list created |V-1| times, that is number of vertices - 1.
To make things simple we will only work with bottom half part of our previous graph with negative weights. If you understand it, it is quite simple to implement on larger graphs.
1. Creating list of edges using bottom half of previous example with negative weight we get
lst = [(A-D), (A-C), (D-C)]
2. Initialize distances.
NOTE: unlike dijkstra directly connected vertices gets assigned infinite number.
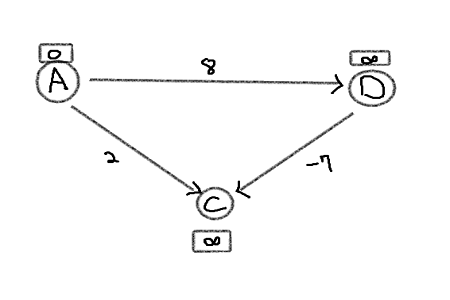
3. going through [(A,D), (A,C). (D,C)] |V-1| = 2 times and perform relaxation.
First looking at (A,D), w(A,D) + d[A] is less than already assigned distance which is infinity thus we relax it.
same for (A,C), w(A,C) + d[A] is less than infinity therefore relax it.
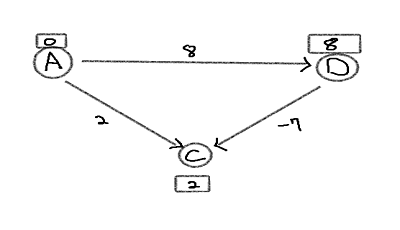
next looking at (D,C), w(D,C) + d[D] = 1, which is smaller than d[C] = 2 so relax it.
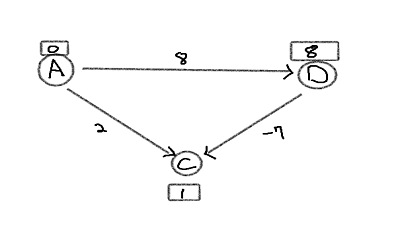
Now repeat the steps one more time as we have to perform it |V-1| times.
(A,D), w(A,D) + d[A] = d[D] so we keep it as is.
(A,C), w(A,C) + d[A] > d[C] so keep it.
(D,C), w(D,C) + d[D] = d[C] so we keep it.
Note that order of edges in list does not matter.
By using Bellman-Ford we check that even though there are negative weights it can correctly update it. However since you need to iterate |V-1| times on number of edges, its time complexity is O(|E|*|V-1|) which is O(n^2) when there are same number of edges as vertices and upto O(n^3) when graph is complete.
Book I am reading "뇌를 자극하는 알고리즘" only covers Dijkstra algorithm however as I was searching the internet about things I was curious about it made this blog too long... for that reason I will split it into two parts, part II consisting all-pairs shortest path algorithms -> Continue straight to part II