Dynamic Programming Introduction:

date posted: 2020-02-22

What is dynamic programming?

Dynamic programming which is named by Bellman Ford in 1952 is a technique used to increase performace in a problem, that can be broken down to subproblems and answers from previous subproblems are used recursively. This is similar to divide and conquer technique since they both break down problem into subproblems and approach smaller problems one by one however in order to increase performance with dynamic programming approach a problem need to have additional condition even though with out the condition a problem can be solved using dynamic programming it wouldn't be efficient.

After all reason for using some kind of technique in computer science is to increase efficiency. In order to benefit from dynamic programming technique a problem should satisfy two additional conditions:

1. Optimal substructure:

   larger/later subproblems require answers from previous sub problem.

2. Overlapping sub-problems:

   subproblems are reused several times

So why so many conditions?
Dynamic programming works in following steps:

1. Split problem into subproblems and order them in "must be solved first" -> "solved last" subproblems
2. Solve from first to last and store answers into a table.
3. Use previous answers stored in table to solve next subproblem and so on

Storing answers from first occuring problems and use stored answer when same problem are being encountered.

Now that you know what dynamic programming is and how to use it, let's find nth fibonacci number using recursive algorithm then improve its performance using two different types of dynamic programming Memoization and Tabulation.

Below is algorithm for finding nth fibonacci number in python.

def fib(n):
    if n<=2: f = 1
    else: f = fib(n-1) + fib(n-2)
    return f

Its performance becomes intuitive if I represent it as a tree.

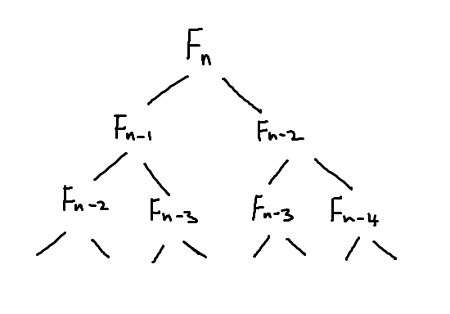
If you want to find Fn then you first need to find Fn-1, Fn-2 and for each of them we need to find two of its previous numbers and so on... As we go down each depth there are 2^n numbers to compute therefore its time complexity would be O(2^n).

Memoization

If we look carefully at our fibonacci tree above we can see there are duplicate values and current problem relies on its previous problem's answer. Doesn't this sound like it satisfy conditions we've described above? Yes it does therefore let's increase performance by using Memoization dynamic programming approach. It is an approach where you are "Memoing" already solved problem so that re-occuring problem's answer can be found from memo.

It is referred to as top-down approach since if you want to find F(n) then we goto F(n-1), F(n-2) then find their previous numbers and so on until very bottom. Even though "dynamic programming" sounds fancy it's very simple. Memoization simply compute a subproblem, store it in a dictionary and return, if it already exists return that value.

memo = {}
    def fib(n):
        if n in memo: return memo[n]
        if n<=2: f = 1
        else: f = fib(n-1) + fib(n-2)
        memo[n] = f
        return f

We've just added 3 lines of code and improved performance from O(2^n) to O(n).

Note that in fibonacci number in order to find Fn we need to compute Fn-1, Fn-2, ... and so on. In recursive algorithm we needed to compute subproblems multiple times however in memoization if we have computed it we never have to compute it again therefore we only need to compute Fn-1, Fn-2, ... F0 only once giving us O(n).

Tabulation

This is bottom-up version of dynamic programming, this time we start by computing F1, F2, F3, and up to Fn. Starting from the bottom we store its number into a table (hence the name Tabulation) and use those value inside table as we move up.

fib_table = {}
def fib(n):
    for k in range(1, n+1):
        if k <=2:
            f=1
        else:
            f = fib_table[k-1] + fib_table[k-2]
        fib_table[k] = f
    return fib_table[n]

Starting from k = 1, f = 1 stored in fibonacci table, next for k=2 stores f = 2 into fibonacci table. Next k = 3 and since we've already stored k=2, k=1 into our fibonacci table we simply use them to find F3. Again we can see that we only need to compute f1,f2, ... upto Fn once therefore giving same time complexity as our top-down approach.

It seems like both top-down and bottom-up give same performance boost then why is there two methods? why not just stick to one?

Tabulation Vs. Memoization

Memoization is preferred when we do not need to know answers to all previous subproblems to solve final problem. In fibonacci numbers we needed to know all of previous subproblems in order to find Fn however if we only need subset of previous subproblems to find final answer we would use memoization technique.

Tabulation is preferred when you need all previous subproblems to find final answer just like in fibonacci numbers.